弧度法の定義
角の大きさの新しい表し方を導入します。
度数法
これまでは1周を360°と定義し、それを基準に角の大きさを表してきました。
これを「度数法」といいます。
しかし、度数法は慣習的なものであり、使い勝手がよくありません。
弧度法
度数法より扱いやすい表し方を導入します。
ここで役に立つのが、「円の弧の長さ」です。
円の中心角の大きさと弧の長さは比例します。
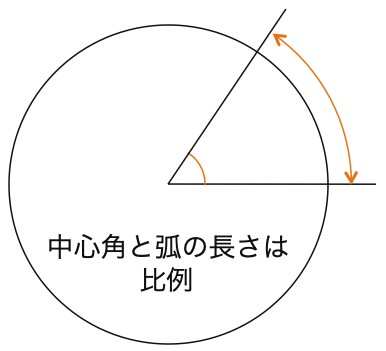
この性質を利用し、角の大きさを弧の長さで表します。
しかし、ここで1つ問題があります。
弧の長さは半径にも比例します。
そのため角の大きさが同じでも、半径が異なると弧の長さも異なってしまいます。
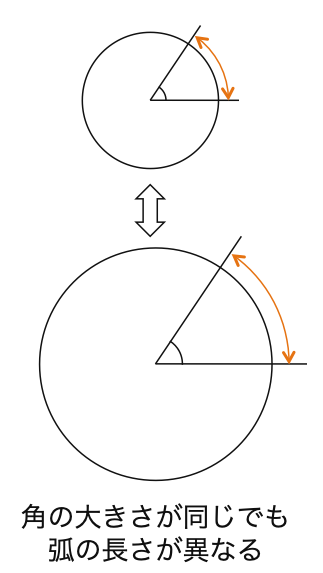
そこで半径を1と指定し、半径1の円の弧の長さで角の大きさを表すこととします。
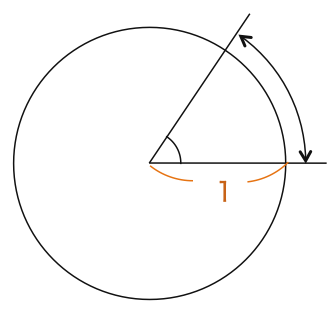
この角の表し方を「弧度法」といいます。
単位は「ラジアン」または「弧度」を用いますが、通常、弧度法の単位は省略されます。
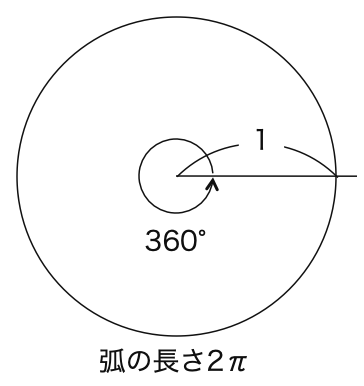
例えば半径1,中心角360°(つまり円)の弧の長さは2πであるため、
360° = 2π ラジアン
となります。
代表的な角を度数法と弧度法で表すと、以下のようになります。
| 度数法 | 0° | 90° | 180° | 360° |
| 弧度法 | 0 | π/2 | π | 2π |
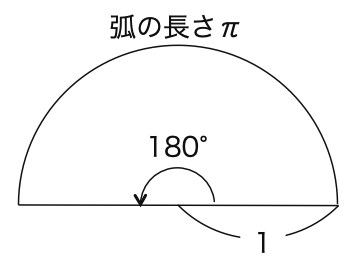
特に180° = π は覚えやすいため,頭に入れておくとよいでしょう。
扇形の弧の長さと面積
弧度法を用いて、扇形の弧の長さと面積を与える式を導きます。
考え方は度数法のときと同じです。
半径がr,中心角がθの扇形の弧の長さをl,面積をSとします。
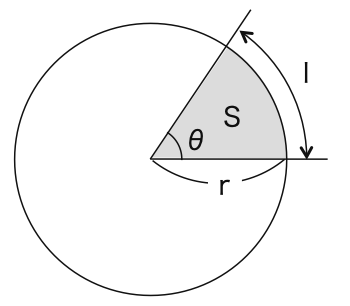
弧の長さ
円(中心角 = 2π)のときの弧の長さは2πrです。
したがって、中心角がθのときの弧の長さlは
l = 2πr × θ/2π = rθ・・・①
となります。
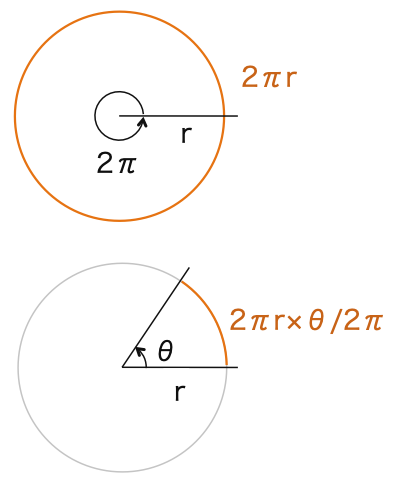
面積
円(中心角 = 2π)のときの面積はπr2です。
したがって、中心角がθのときの面積Sは
S = πr2 × θ/2π = r2θ/2・・・②
となります。
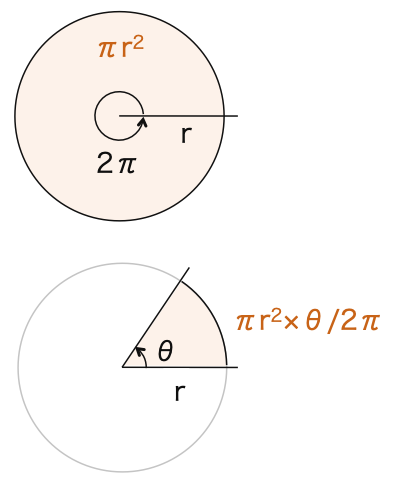
また、①,②から
S = rl/2・・・③
が成り立ちます。
①,②,③は公式として覚えるまでもないと思います。
まとめ
- 半径1の円の弧の長さを用いて角の大きさを表す方法を、弧度法という。
- 180° = πラジアンを覚えておくとよい。
- 扇形の弧の長さ、面積は度数法のときと同じ考え方で導き出せる。
問題
問1
次の角を弧度法で表せ。
(1)30°
(2)-300°
問2
次の角を度数法で表せ。
(1)2π/3
(2)-5π/12
問3
次の扇形の弧の長さと面積を求めよ。
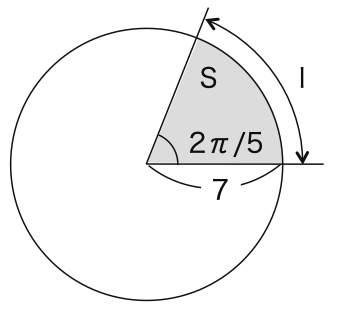
半径が7,中心角が2π/5
問1
半径1の円の弧の長さを求めればよいです。
(1)2π×1×30°/360° = π/6
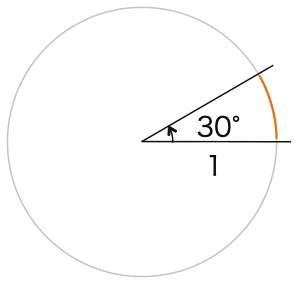
(2)2π×1×(-300°)/360° = -5π/3
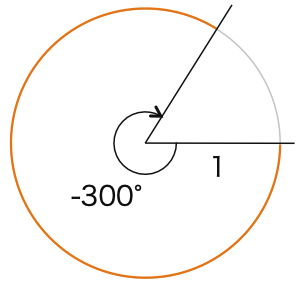
180° = πを覚えていれば、より早く解けます。
(1)π×30°/180° = π/6
(2)π×(-300°)/360° = -5π/3
問2
半径1の円の、弧の長さに対応する角を求めればよいです。
(1)
1周(360°)の弧の長さは2πです。

したがって、弧の長さが2π/3のときの中心角は
360°×(2π/3)/2π = 120°
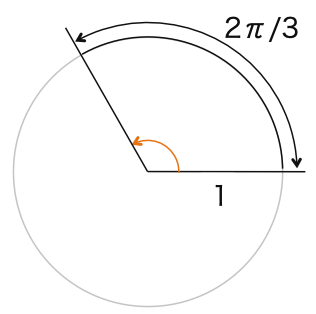
(2)
1周(360°)の弧の長さは2πです。

したがって、弧の長さが-5π/12のときの中心角は
360°×(-5π/12)/2π = -75°
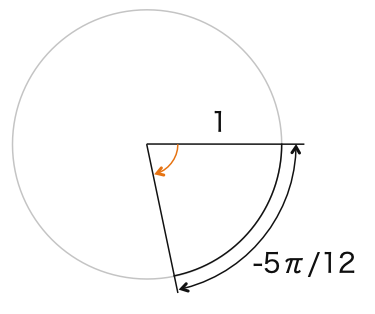
180° = πを覚えていれば、より早く解けます。
(1)2π/3×180°/π = 120°
(2)-5π/12×180°/π = -75°
問3
半径が7,中心角が2π/5の扇形の弧の長さをl,面積をSとすると、
l = 2π×7×(2π/5)/2π = 14π/5
S = π×72×(2π/5)/2π = 49π/5