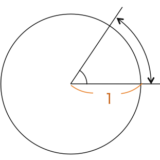
図形に現れる角の大きさは0°から360°まででですが、例えば時計の針のような回転を扱う場合、1周(360°)を超えてさらに回ることができます。
また、時計回り・反時計回りといった回転の向きも存在します。
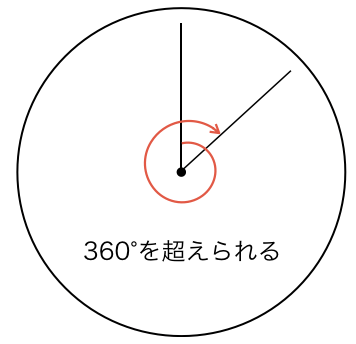
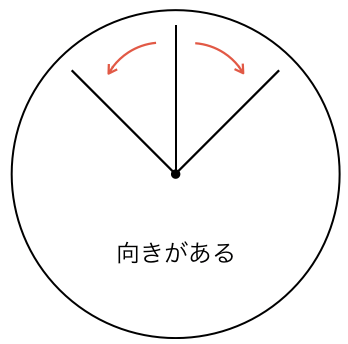
このような、回転に関する範囲と向きまで考えて意味を広げた角を「一般角」といいます。
以下に一般角に関する定義を述べます。
回転に関する言葉の定義
平面上で、点Oを中心に半直線OPを回転させるとき、この半直線OPを「動径」といいます。

また、動径の最初の位置を示す半直線OXを「始線」といい、始線を基準とした動径の回転角を考えます。
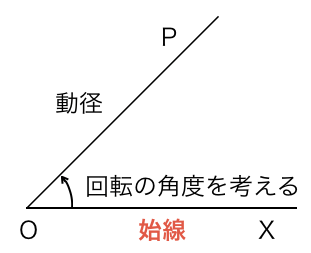
向きの定義
反時計回りが正の向き、時計回りが負の向きと定義されています。
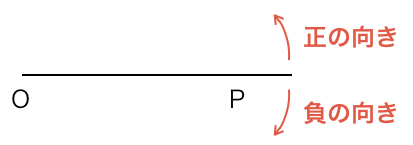
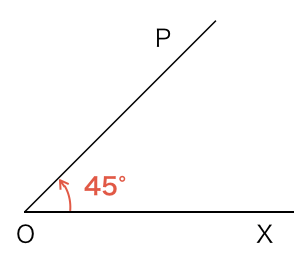
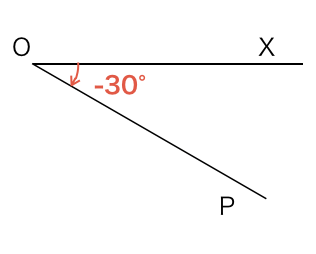
例えば反時計回りに45°回転したときは+45°または単に45°、時計回りに30°回転したときは−30°と表します。
360°より大きい角の表し方
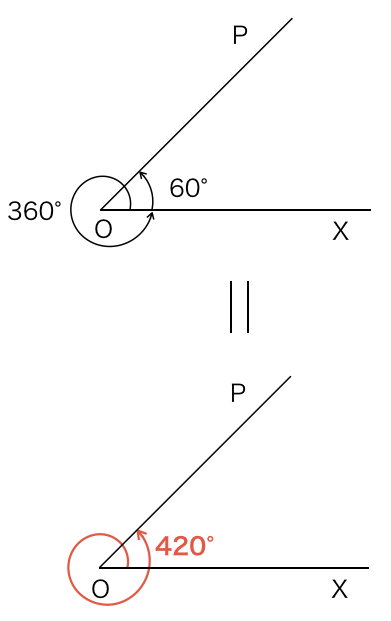
単純に、回転した角度をそのまま表します。
例えば、360°回転した後さらに60°回転した場合、360+60=420より420°と表します。
動径の表す角
動径は360°回転すると元の位置に戻ります。
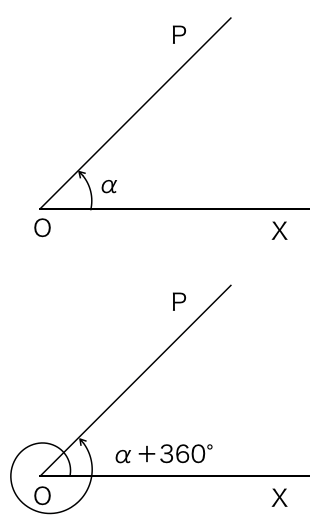
したがって、例えばある角αの動径があるとき、以下の角の動径はすべて一致します。
α+360°
α+360°×2
α+360°×3
・・・
α+360°×(ー1)
α+360°×(ー2)
α+360°×(ー3)
・・・
これらの無数の角を「動径OPの表す角」といいます。
つまり、ある角αの動径が与えられたとき、その動径の表す角θは1つに定まりません。
そこで、それらをまとめて以下のように表します。
θ=α+360°×n(nは整数)
まとめ
- 範囲と方向について意味を広げた角を「一般角」といいます。
- 回転する半直線を「動径」、動径の最初の位置を示す半直線を「始線」といい、始線を基準とした動径の回転角を考えます。
- 反時計回りが正の向き、時計回りが負の向きと定義されています。
- 360°より大きい角はそのまま表します。
- 動径OPの表す角はまとめて以下のように表します。
θ=α+360°×n(nは整数)
練習問題
問1
次の角の動径を図示せよ。
(1)510°
(2)-270°
問2
次の角のうち、その動径が30°の動径と一致するものはどれか。
100°,750°,-330°,-670°,-30°,1110°
問1
(1)
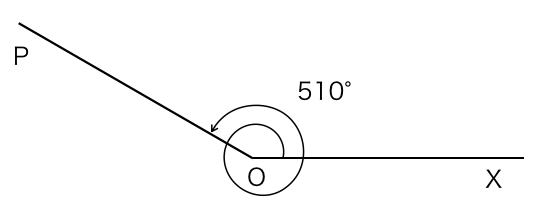
(2)
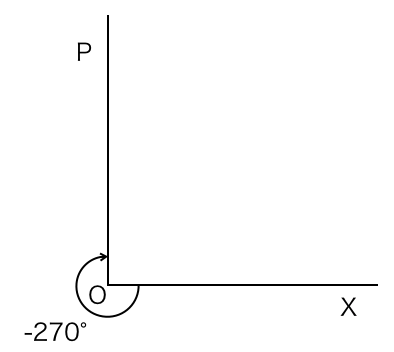
問2
【答え】
750°,-330°,1110°
【解説】
与えられた角をθとすると、θが
θ=30°+360°×n(nは整数)・・・式①
を満たすとき、その動径は30°の動径と一致します。
よって、以下の3つの角が30°の動径と一致します。
750°=30°+360°×2
-330°=30°+360°×(-1)
1110°=30°+360°×3
実際に問題を解くときは、以下の手順を踏めば良いと思います。
- 式①を変形して
n=(θ-30°)/360°(nは整数)・・・式②
とする。 - それぞれの角を式②のθに代入し、右辺が整数になるものを選ぶ。
あるいは、それぞれの動径を図示しながら考えてもいいかもしれません。