【共通テスト｜解答・解説】 2022年度 数学ⅠA 第3問

共通テスト 2022年度 数学ⅠA 第3問の解き方を解説します。

手順１：問題文を通して読む

問題を解く前に、問題文を通して読みましょう。

手順２：文脈を理解し、解き方を予想する

問題文の流れを理解し、解き方を予想しましょう。

【予想】
場合分けを書き出す。

【予想】
構想に書かれている手順で問題を解く。

• 自分のプレゼントを受け取る人の人数で場合分けし、それぞれの場合が何通りあるか求める。
• 終了しないパターンの総数を求める。
• （終了する総数） ＝ （全パターン） − （終了しない場合の総数）を求める。

（サ）（シ）は人数で場合分けして何通りであるか求める。
終了しないパターンをそれぞれ求め、総数（スセ）を求める。
（終了する総数） ＝ （全パターン） − （終了しない場合の総数）により、終了する総数、さらに終了する確率\(\displaystyle \frac{（ソ）}{（タ）}\)を求める。

【予想】
（2）と同じ手順を使う。

【予想】
Eが自分のプレゼントを受け取らなければ終了する。
Eが自分のプレゼントを受け取る場合と、受け取らない場合を考える。

手順３：問題を解く

(ⅰ)　
２人で交換会を開く場合のプレゼント受け取り方を書き出す。２人の名前をA・B、
それぞれのプレゼントをa・bとする。プレゼントの受け取り方は、以下の通りである。

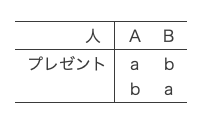
以下に、自分のプレゼントを受け取った場合を丸で囲んで示す。

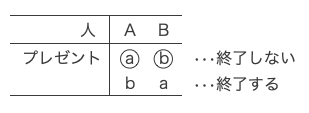
したがって、プレゼントの受け取り方の総数は２、その内、交換会が終了する場合の総数は１である。
よって、1回目の交換で交換会が終了する確率は\(\displaystyle \frac{1}{2} \)である。••• ア

(ⅱ)
３人で交換会を開く場合のプレゼント受け取り方を書き出す。２人の名前をA・B・C、
それぞれのプレゼントをa・b・cとする。プレゼントの受け取り方は、以下の通りである。
自分のプレゼントを受け取った場合を○で囲んで示した。

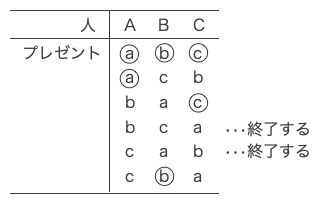
したがって、プレゼントの受け取り方の総数は６、その内、交換会が終了する場合の総数は２である。
よって、1回目の交換で交換会が終了する確率は\(\displaystyle \frac{2}{6} = \frac{1}{3}\)である。••• イ

(ⅲ)　
4回以下の交換で交換会が終了するときは、1回、2回、3回、4回で交換が終了する場合に分けられる。
ゆえに、4回以下の交換で交換会が終了する確率は、1回、2回、3回、4回で交換が終了する確率の
合計である。

(ⅱ)より、各回で終了する確率は\(\displaystyle \frac{1}{3} \)、終了しない確率は\(\displaystyle \frac{2}{3} \)であるから、各場合の確率は以下のように求められる。

よって、4回以下で終了する確率は、\(\displaystyle \frac{1}{3}+\frac{2}{3}\times\frac{1}{3}+\left(\frac{2}{3}\right)^2\times\frac{1}{3}+\left(\frac{2}{3}\right)^3\times\frac{1}{3}=\frac{65}{81} \)である。••• キクケコ

４人の名前をA・B・C・D、それぞれのプレゼントをa・b・c・dとする。
1人が自分の持参したプレゼントを受け取る場合を考える。
まず、自分のプレゼント受け取る1人の選び方は、以下の４通りである。

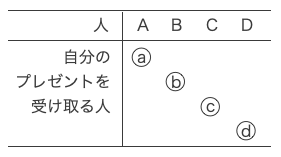
この中で、Aが自分のプレゼントを受け取った場合を考える。

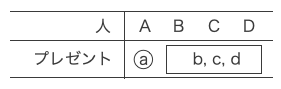
B・C・Dは自分のプレゼントを受け取らない。これは(1)(ⅱ)で交換会が終了する場合と同じ状況である。
ゆえにB・C・Dのプレゼントの受け取り方は２通りである。
よって、1人が自分のプレゼントを受け取る場合は\( 4\times2= 8 \)通りである。••• サ

２人が自分の持参したプレゼントを受け取る場合を考える。
まず、自分のプレゼント受け取る２人の選び方は、\(\displaystyle {}_4C_2=\frac{4\times3}{2\times1}\)=６通りである。

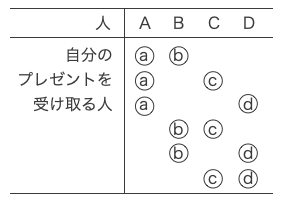
この中で、AとBが自分のプレゼントを受け取った場合を考える。

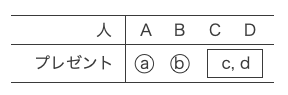
C・Dは自分のプレゼントを受け取らない。これは(1)(ⅰ)で交換会が終了する場合と同じ状況である。
ゆえにC・Dのプレゼントの受け取り方は１通りである。
よって、1人が自分のプレゼントを受け取る場合は\( 6\times1= 6 \)通りである。••• シ

３人が自分の持参したプレゼントを受け取る場合を考える。
この場合、残りの1人も自分のプレゼントを受け取ることになり、以下の１通りのみである。

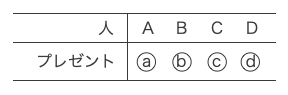
よって、1回目の交換で交換会が終了しない受け取り方の総数は、8+6+1=15通りである。•••スセ

交換が終了する確率を求める。
受け取り方の総数は4×3×2×1=24通り、終了しない受け取り方の総数は15通りであるから、
終了する受け取り方の総数は\(24-15=9\)通りである。
よって、終了する確率は\(\displaystyle \frac{9}{24}=\frac{3}{8}\)である。•••ソタ

ここまでの内容をまとめると、以下のようになる。

５人の名前をA・B・C・D・E、それぞれのプレゼントをa・b・c・d・eとする。
（2）と同じ手順で解く。
1人が自分の持参したプレゼントを受け取る場合を考える。
まず、自分のプレゼント受け取る1人の選び方は、以下の５通りである。

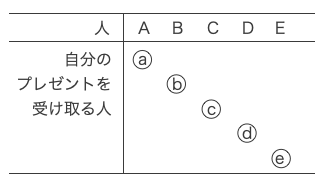
この中で、Aが自分のプレゼントを受け取った場合を考える。

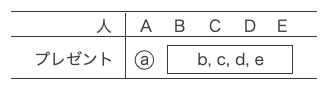
B・C・D・Eは自分のプレゼントを受け取らない。これは(2)で交換会が終了する場合と同じ状況である。
ゆえにB・C・D・Eのプレゼントの受け取り方は９通りである。
よって、1人が自分のプレゼントを受け取る場合は\( 5\times9= 45 \)通りである。

２人が自分の持参したプレゼントを受け取る場合を考える。
まず、自分のプレゼント受け取る２人の選び方は、\(\displaystyle {}_5C_2=\frac{5\times4}{2\times1}\)=10通りである。

この中で、AとBが自分のプレゼントを受け取った場合を考える。

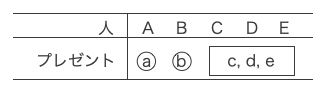
C・D・Eは自分のプレゼントを受け取らない。これは(1)(ⅱ)で交換会が終了する場合と同じ状況である。
ゆえにC・D・Eのプレゼントの受け取り方は２通りである。
よって、２人が自分のプレゼントを受け取る場合は\( 10\times2= 20 \)通りである。

３人が自分の持参したプレゼントを受け取る場合を考える。
まず、自分のプレゼント受け取る３人の選び方は、\(\displaystyle {}_5C_3=\frac{5\times4\times3}{3\times2\times1}\)=10通りである。

この中で、AとBとCが自分のプレゼントを受け取った場合を考える。

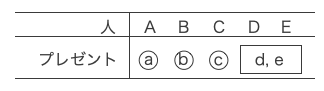
D・Eは自分のプレゼントを受け取らない。これは(1)(ⅰ)で交換会が終了する場合と同じ状況である。
ゆえにD・Eのプレゼントの受け取り方は１通りである。
よって、２人が自分のプレゼントを受け取る場合は\( 10\times1= 10 \)通りである。

４人が自分の持参したプレゼントを受け取る場合を考える。
この場合、残りの1人も自分のプレゼントを受け取ることになり、以下の１通りのみである。

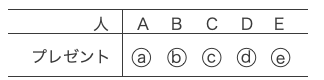
よって、1回目の交換で交換会が終了しない受け取り方の総数は、45+20+10+1=76通りである。

交換が終了する確率を求める。
受け取り方の総数は5×4×3×2×1=120通り、終了しない受け取り方の総数は76通りであるから、
終了する受け取り方の総数は\(120-76=44\)通りである。
よって、終了する確率は\(\displaystyle \frac{44}{120}\)である。•••チツテト

ここまでの内容をまとめると、以下のようになる。

A・B・C・D・Eのそれぞれのプレゼントを、a・b・c・d・eとする。
A・B・C・Dが自分以外の人のプレゼントを受け取った時、その回で交換会が終了するには、
Eも自分以外の人のプレゼントを受け取ることが必要である。
逆に、Eが自分のプレゼントを受け取った場合は、終了しない。

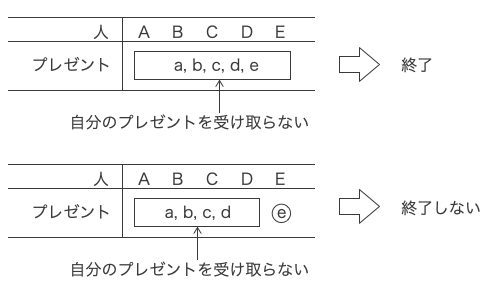
Eも自分以外の人のプレゼントを受け取る場合、（3）と同じ状況であるから、受け取り方は44通りである。
また、Eが自分のプレゼントを受け取る場合、（2）と同じ状況であるから、受け取り方は9通りである。
よって、交換が終了する確率は、\(\displaystyle \frac{44}{44+9}=\frac{44}{53}\) ••• ナニヌネ

他の問題の解説