共通テスト 2022年度 数学ⅠA 第5問の解き方を解説します。
目次
手順1:問題文を通して読む
問題を解く前に、問題文を通して読みましょう。
手順2:文脈を理解し、解き方を予想する
問題文の流れを理解し、解き方を予想しましょう。
【問題文】
(1)
△ABCの形状に関係なく
\(\displaystyle \frac{AD}{DE}=\frac{\text{(ア)}}{\text{(イ)}}\)
である。また、点Fの位置に関係なく
\(\displaystyle \frac{BP}{AP}=\text{(ウ)}\times\frac{\text{(エ)}}{\text{(オ)}},
\frac{CQ}{AQ}=\text{(カ)}\times\frac{\text{(キ)}}{\text{(ク)}}\)
であるので、つねに
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=\text{(ケ)}\)
となる。
【予想】
まずは図を描く。
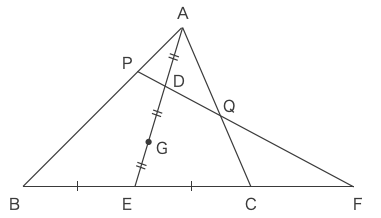
\(\displaystyle \frac{AD}{DE}\):図からすぐに分かる。
\(\displaystyle \frac{BP}{AP},\,\frac{CQ}{AQ}\):2つの三角形が重なった形で、線分の比を求める。
→ メネラウスの定理を使う。
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}\):前で求めた式を足してみる。
【問題文】
(2)
\(\displaystyle AQ=\frac{\text{(コ)}}{\text{(サ)}}AP\)であるから
\(\displaystyle AP=\frac{\text{(シス)}}{\text{(セ)}},\,AQ=\frac{\text{(ソタ)}}{\text{(チ)}}\)
であり
\(\displaystyle CF=\frac{\text{(ツテ)}}{\text{(トナ)}}\)
である。
【予想】
まずは図を描く。
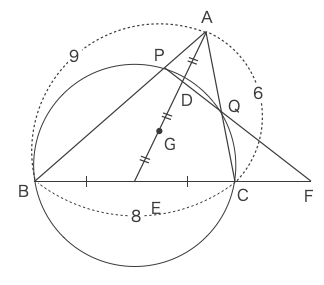
\(\displaystyle AQ=\frac{\text{(コ)}}{\text{(サ)}}AP\):円と三角形が重なった形で、交点までの線分の長さの比を求める。
→ 方べきの定理を使う。
\(\displaystyle AP=\frac{\text{(シス)}}{\text{(セ)}},\,AQ=\frac{\text{(ソタ)}}{\text{(チ)}}\):前に出てきた式を使う。
\(\displaystyle CF=\frac{\text{(ツテ)}}{\text{(トナ)}}\):ここまでで長さがわかっている線分を用いて、CFの長さを求める。
→ メネラウスの定理を使う。
【問題文】
(3)
つねに\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=10\)となるのは、\(\displaystyle \frac{AD}{DG}=\frac{\text{(ニ)}}{\text{(ヌ)}}\)のときである。
【予想】
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}\), \(\displaystyle \frac{AD}{DG}\)が出てきているため、(1)を利用すると予想する。
手順3:問題を解く
【問題文】
(1)
△ABCの形状に関係なく
\(\displaystyle \frac{AD}{DE}=\frac{\text{(ア)}}{\text{(イ)}}\)
である。また、点Fの位置に関係なく
\(\displaystyle \frac{BP}{AP}=\text{(ウ)}\times\frac{\text{(エ)}}{\text{(オ)}},
\frac{CQ}{AQ}=\text{(カ)}\times\frac{\text{(キ)}}{\text{(ク)}}\)
であるので、つねに
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=\text{(ケ)}\)
となる。
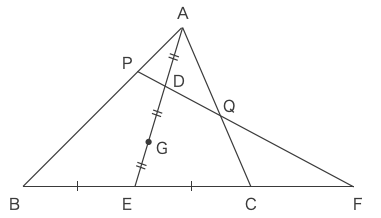
点Gが△ABCの重心であるから、\(AG:GE=2:1\)である。
従って、点Dが線分AGの中点であるとき、\(AD=DG=GE\)であり、\(\displaystyle \frac{AD}{DE}=\frac{1}{2}\)である。••• アイ
\(\displaystyle \frac{BP}{AP}\)を求める。
前の式(\(\displaystyle \frac{AD}{DE}=\frac{1}{2}\))が誘導になっている。
\(\displaystyle \frac{AD}{DE}\)がわかっており、\(\displaystyle \frac{BP}{AP}\)を求める。
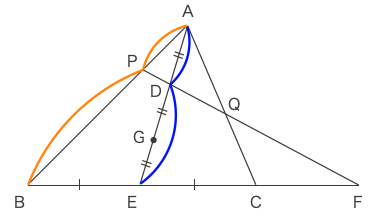
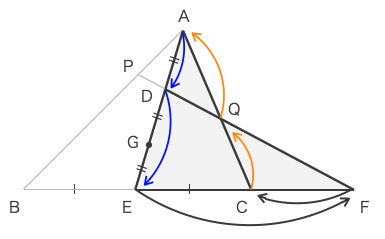
ゆえに、以下の灰色の塗りで示した図に対しメネラウスの定理を用いれば良いとわかる。
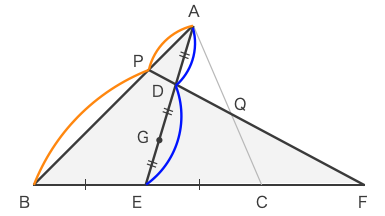
メネラウスの定理より、\(\displaystyle \frac{AP}{PB}\cdot\frac{BF}{FE}\cdot\frac{ED}{DA}=1\)
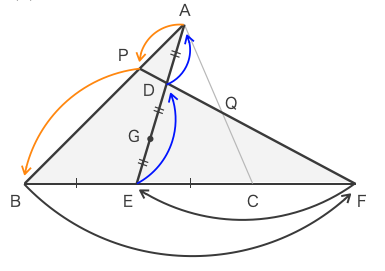
ゆえに
\(\displaystyle \frac{AP}{PB}\cdot\frac{BF}{FE}\cdot\frac{2}{1}=1\)
\(\displaystyle \frac{AP}{PB}=\frac{FE}{BF}\cdot\frac{1}{2}\)
\(\displaystyle \frac{BP}{AP}=2\times\frac{BF}{EF}\) (選択肢 ①, ③)••• ウエオ
\(\displaystyle \frac{BP}{AP}\)を求める。
前の式(\(\displaystyle \frac{AD}{DE}=\frac{1}{2}\))が誘導になっている。
\(\displaystyle \frac{AD}{DE}\)がわかっており、\(\displaystyle \frac{CQ}{AQ}\)を求める。
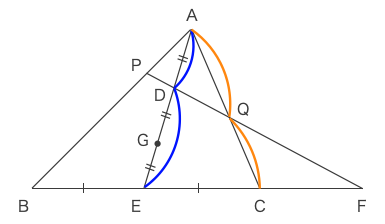
ゆえに、以下の灰色の塗りで示した図に対しメネラウスの定理を用いれば良いとわかる。
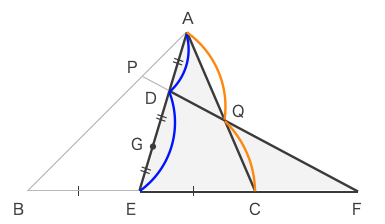
メネラウスの定理より、\(\displaystyle \frac{AD}{DE}\cdot\frac{EF}{FC}\cdot\frac{CQ}{QA}=1\)
ゆえに
\(\displaystyle \frac{1}{2}\cdot\frac{EF}{FC}\cdot\frac{CQ}{QA}=1\)
\(\displaystyle \frac{CQ}{QA}=\frac{2}{1}\cdot\frac{FC}{EF}=2\times\frac{CF}{EF}\)(選択肢 ②, ③)••• カ, キ, ク
わかっている情報と求めなければならない情報から、用いる定理を決める。
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}\)を求める。
前の式を足す。
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=2\times\frac{BF}{FE}+2\times\frac{CF}{EF}=2\times\frac{BF+CF}{EF}\)
ここで、\(\displaystyle \frac{BF+CF}{EF}\)を求める。
\(BE=EC=x, CF=y\)とすると、\(BF=2x+y, CF=y, EF=x+y\)である。
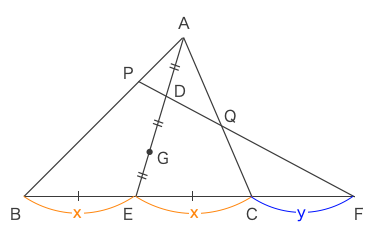
ゆえに、\(\displaystyle \frac{BF+CF}{EF}=\frac{2x+y+y}{x+y}=\frac{2(x+y)}{x+y}=2\)
よって、
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=2\times\frac{BF+CF}{EF}=2\times2=4\)••• ケ
線分の長さを文字で置いて、式で表してみる。
【問題文】
(2)
\(\displaystyle AQ=\frac{\text{(コ)}}{\text{(サ)}}AP\)であるから
\(\displaystyle AP=\frac{\text{(シス)}}{\text{(セ)}},\,AQ=\frac{\text{(ソタ)}}{\text{(チ)}}\)
であり
\(\displaystyle CF=\frac{\text{(ツテ)}}{\text{(トナ)}}\)
である。
AQとAPの比を求める。
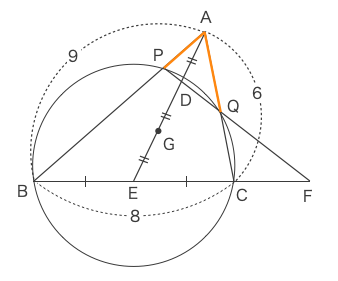
三角形の頂点から、円との交点までの長さの比を求めるため、方べきの定理を使う。
方べきの定理より、\({AP}\cdot{AB}={AQ}\cdot{AC}\)
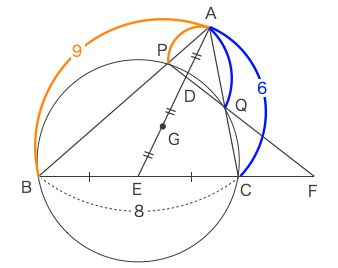
ゆえに
\(\displaystyle AQ=\frac{AB}{AC}\cdot{AP}=\frac{9}{6}\cdot{AP}=\frac{3}{2}\cdot{AP}\) ••• コ, サ
わかっている情報と求めなければならない情報から、用いる定理を決める。
AP, AQを求める。
前の式から使えそうなものを探す。
\(\displaystyle \frac{BP}{AP}=2\times\frac{BF}{EF}\), \(\displaystyle \frac{CQ}{QA}=2\times\frac{CF}{EF}\) はBF,EF,CFが不明のため使えない。
(問題文では、このあとCFを求めることになっている。)
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=4\)は、以下のように各値をAPで表せるため使える。
\(BP=AB-AP=9-AP\)
\(\displaystyle CQ=AC-AQ=6-\frac{3}{2}AP\)
\(\displaystyle AQ=\frac{3}{2}AP\)
ゆえに
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=4\)
\(\displaystyle \frac{9-AP}{AP}+\frac{6-\frac{3}{2}AP}{\frac{3}{2}AP}=4\)
両辺に \(\displaystyle \frac{3}{2}AP\)をかけると
\(\displaystyle \frac{3}{2}(9-AP)+\left(6-\frac{3}{2}AP\right)=4\cdot\frac{3}{2}AP\)
両辺に2をかけると
\(\displaystyle 3(9-AP)+(12-3AP)=4\cdot{3AP}\)
\(27-3AP+12-3AP=12AP\)
\(39=18AP\)
\(\displaystyle AP=\frac{39}{18}=\frac{13}{6}\) •••シ, ス, セ
また、 \(\displaystyle AQ=\frac{3}{2}AP=\frac{3}{2}\times\frac{13}{6}=\frac{13}{4}\) •••ソ, タ, チ
前問を参考にする。
CFを求める。
前の式から使えそうなものを探す。
\(\displaystyle \frac{BP}{AP}=2\times\frac{BF}{EF}\), \(\displaystyle \frac{CQ}{AQ}=2\times\frac{CF}{EF}\) のどちらも使えるが、ここでは \(\displaystyle \frac{CQ}{AQ}=2\times\frac{CF}{EF}\)を用いる。
各値は以下のように表せる。
\(\displaystyle CQ=6-AQ=6-\frac{13}{4}=\frac{11}{4}\)
\(\displaystyle AQ=\frac{13}{4}\)
\(EF=EC+CF=4+CF\)
ゆえに\(\displaystyle \frac{CQ}{AQ}=2\times\frac{CF}{EF}\)にこれらを代入して解くと、
\(\displaystyle \frac{\frac{11}{4}}{\frac{13}{4}}=2\times\frac{CF}{4+CF}\)
\(\displaystyle \frac{11}{13}=2\times\frac{CF}{4+CF}\)
\(\displaystyle \frac{11}{13}(4+CF)=2CF\)
\(\displaystyle \frac{44}{13}+\frac{11}{13}CF=2CF\)
\(\displaystyle \frac{44}{13}=\frac{15}{13}CF\)
\(44=15CF\)
よって、\(\displaystyle CF=\frac{44}{15}\) ••• ツ, テ, ト, ナ
前問を参考にする。
【問題文】
(3)
つねに\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=10\)となるのは、\(\displaystyle \frac{AD}{DG}=\frac{\text{(ニ)}}{\text{(ヌ)}}\)のときである。
つねに\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=10\)となる\(\displaystyle \frac{AD}{DG}\)を求める。
これらの式が使われている(1)を使うと予想できる。
(1)の計算の流れは、以下のようになっている。
- \(\displaystyle \frac{AD}{DE}\)の値を求める。
- メネラウスの定理を用いて、\(\displaystyle \frac{BP}{AP}\)と\(\displaystyle \frac{CQ}{AQ}\)を求める。
- これらを足し合わせて\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}\)を求める。
これと同様に、以下の手順で\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=10\)となる\(\displaystyle \frac{AD}{DG}\)を求める。
- \(\displaystyle \frac{AD}{DE}\)の値をaと仮定する。
- メネラウスの定理を用いて、\(\displaystyle \frac{BP}{AP}\)と\(\displaystyle \frac{CQ}{AQ}\)をaを用いて表す。
- これらを足し合わせて、\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}\)をaを用いて表す。
- \(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=10\)となるaを求める。
- このときの\(\displaystyle \frac{AD}{DG}\)を求める。
\(\displaystyle \frac{AD}{DE}=a\)とすると、メネラウスの定理より
\(\displaystyle \frac{AP}{PB}\cdot\frac{BF}{FE}\cdot\frac{ED}{DA}=1\)
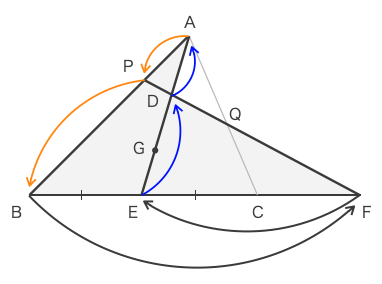
\(\displaystyle \frac{AP}{PB}\cdot\frac{BF}{FE}\cdot\frac{1}{a}=1\)
\(\displaystyle \frac{AP}{PB}=a\cdot\frac{FE}{BF}\)
\(\displaystyle \frac{BP}{AP}=\frac{1}{a}\cdot\frac{BF}{EF}\)
また、メネラウスの定理より
\(\displaystyle \frac{AD}{DE}\cdot\frac{EF}{FC}\cdot\frac{CQ}{QA}=1\)
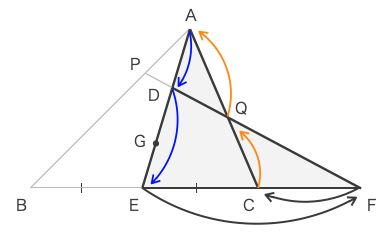
\(\displaystyle a\cdot\frac{EF}{FC}\cdot\frac{CQ}{QA}=1\)
\(\displaystyle \frac{CQ}{QA}=\frac{1}{a}\cdot\frac{FC}{EF}\)
ゆえに、
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=\frac{1}{a}\cdot\frac{FC}{EF}+\frac{1}{a}\cdot\frac{BF}{EF}=\frac{1}{a}\cdot\frac{FC+BF}{EF}=\frac{2}{a}\)
\(\displaystyle \frac{BP}{AP}+\frac{CQ}{AQ}=\frac{2}{a}=10\)となるaは、
\(\displaystyle a=\frac{2}{10}=\frac{1}{5}\)である。
aすなわち\(\displaystyle \frac{AD}{DE}\)が\(\displaystyle \frac{1}{5}\)であるときの、\(\displaystyle \frac{AD}{DG}\)を求める。
AEを用いて、ADとDGを表す。
\(\displaystyle \frac{AD}{DE}=\frac{1}{5}\)より、
\(\displaystyle AD=\frac{1}{6}AE\)
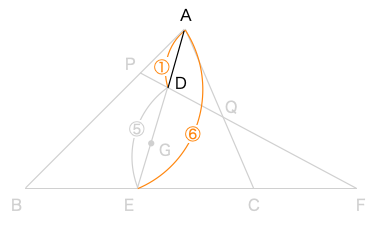
また、\(\displaystyle AG=\frac{2}{3}AE\)である。
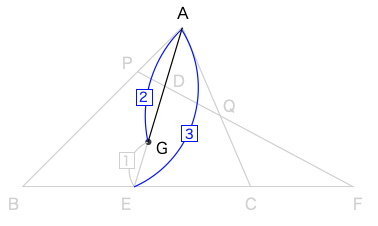
ゆえに、
\(\displaystyle DG=AG-AD=\frac{2}{3}AE-\frac{1}{6}AE=\frac{4-1}{6}AE=\frac{1}{2}AE\)
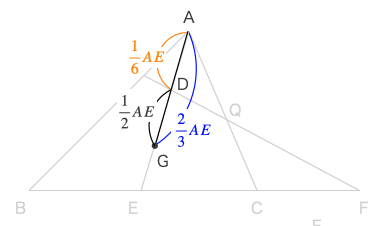
よって、
\(\displaystyle \frac{AD}{DG}=\frac{\frac{1}{6}AE}{\frac{1}{2}AE}=\frac{1}{3}\) •••ニ, ヌ
前問を参考にする。
[…] 第5問 […]
[…] 第5問 […]
[…] 第5問 […]